研究背景

材料科学中，神经网络（NN）、随机森林（Random Forest）、核回归（kernel regression）等机器学习模型已广泛应用于预测材料性质。然而，这些“黑箱”模型缺乏可解释性，难以揭示其预测的物理机制。对于非线性机器学习模型，事后解释技术如SHAP、LIME等可缓解这一问题，但大多数回归模型仍然是黑匣子，没有对其预测的明确解释。因此，构建本质可解释的模型成为更直接的解决方案，保持预测精度的同时增强模型透明度，平衡“预测效率”与“科学解释”的双重需求，为材料设计提供更可靠的物理见解。

前言

机器学习模型可以提供对材料特性的快速准确预测，但通常缺乏透明度。可解释性技术可以与黑盒解决方案一起使用，或者可以创建直接可解释的模型。我们重新审视了几项工作中使用的材料数据集，并证明可以创建非线性基函数的简单线性组合，其准确性与最初使用的内核和神经网络方法相当。线性解可以准确预测透明导电氧化物的带隙和形成能、过渡金属配合物的自旋态以及钠钙镁石结构的形成能。我们演示了线性解决方案如何提供可解释的预测模型，并强调了当可以从模型的系数和函数形式中直接理解模型时可以发现的新见解。此外，我们还讨论了如何识别何时本质上可解释的解决方案可能是实现可解释性的最佳途径。

亮点总结

1.   可解释模型的创新构建：提出“线性组合非线性基函数”框架，将核方法或神经网络中的隐含非线性关系显式转化为带交互项的线性模型，模型系数直接对应物理变量的贡献。

2.   物理机理驱动的特征工程：采用n-gram表示法描述材料局部原子环境，通过LASSO稀疏化筛选关键特征，将材料结构离散化为可解释的团簇贡献，验证了在明确识别空间群无关的全局规律方面的优势。

3.   跨领域方法迁移与验证：推广线性模型至elpasolite晶体（ABC₂D₆）和过渡金属配合物自旋态预测，在保持与黑箱模型相近预测性能的同时，其系数分别反映元素周期表趋势与符合配体场理论。

4.   方法论范式革新：提出“问题适配”原则：离散变量如元素类型等，或小数据集适合线性模型，而连续复杂系统（如原子势）仍需非线性方法，证明PD/ICE可视化可辅助线性模型构建，但直接线性化更高效。

文章介绍

使用神经网络（NN）、随机森林和核回归的预测模型已应用于物理科学，在许多领域取得了巨大成功。然而，解释这些类型的“黑盒”模型的工作原理可能具有挑战性。机器学习可解释性方法可以帮助我们理解机器学习模型，但这些技术存在局限性。另一种方法是将模型重新表述为本质上可解释的模型，而不是在复杂的机器学习解决方案中使用可解释性技术。只要底层基础仍然是可解释的，并且解不是太复杂，非线性基函数的简单线性组合（我们称之为线性模型）是可解释预测的极好方法。在这项工作中，我们重点介绍的例子是使用了核方法或神经网络，但存在其他直接可解释解决方案的示例。在此过程中，我们展示了在可能的情况下转向更简单的回归模型的优势。此外，我们还讨论了如何识别无需复杂非线性解即可描述的一组问题，以及创建本质上可解释模型的替代方法。

多年来，使用机器学习预测材料特性一直是材料科学界感兴趣的主题。了解这些预测模型的工作原理也非常重要。在模型本身的开发中考虑了可解释性；示例包括基于规则的描述符和符号回归。这些是本质上可解释的模型，不需要进一步的处理步骤进行分析。SISSO（确定独立性筛选和稀疏运算符）的发展可以在该领域特别有影响力，它可以从物理特性自动创建解析公式。事后可解释性方法可用于在拟合非线性机器学习模型后对其进行分析。然而，大多数机器学习回归模型仍然是黑匣子，没有对其预测的明确解释。

我们考虑了NOMAD中Kaggle竞赛的获胜模型。该竞赛涉及预测一组透明导电氧化物（TCO）的相对形成能和电子带隙能，特别是Al_xGa_yIn_z)₂O₃化合物（x + y + z = 1）。获胜组使用了核岭回归（KRR）模型。然而，虽然KRR模型可以根据与其他数据点的相似性来解释预测，但使用KRR构建的模型不提供非线性或存在的交互的描述，也没有给出每个变量对结果的贡献的细分。我们首先考虑 NOMAD Kaggle竞赛的获胜解决方案中使用的表示与集群扩展方法之间的联系。然后，我们证明具有成对交互项的线性模型可以预测TCO的形成能和带隙能，其准确性与最初使用的核方法相同。

在重新访问数据集之前，重要的是要考虑可解释性的含义。可解释性是一个概念，其定义不仅特定于给定领域，甚至特定于给定的论文。尽管已经采取措施试图澄清可解释性的含义，但缺乏明确的一般定义。在这项工作中，我们将创建的线性解决方案称为可解释的，因为由于函数形式的简单性，可以实现对全局模型的整体理解，并且单个预测可以分解为来自变量和交互的贡献。然而，由于可解释性是一个主观的和依赖于字段的概念，因此会存在其他观点，特别是关于模型所需的稀疏性。随着该领域的进一步发展，可能会达成更大的共识；但目前不能严格定义模型是否可解释。

围绕可解释性的问题延伸到围绕其好处的讨论。可以说明优势，例如提高科学理解、信任、新的化学和物理见解以及增加知识。然而，我们不是关注不确定的概念，而是确定了一组特征和相关优势：

1）通过分析线性模型的系数，可以看出模型是否同意或不一致已知的物理原理。正如我们将要展示的，这可以作为身体行为的一种验证测试形式。例如，从创建的线性模型的系数中可以看出元素周期表中elpasolite形成能量的预期趋势。

2）通过清晰的函数形式，可以看到模型中存在的假设。这使我们能够将新解决方案与现有的预测模型进行比较，并识别存在的物理假设。这可以指示模型在哪些情况下有效或失败。通过将TCO的解决方案重新制定为专门的线性模型，可以识别与集群扩展（材料建模中的一种既定方法）的相似之处和不同之处，并且可以预测模型将准确描述的系统。

3）线性模型的系数可以提供可用于指导未来预测的信息。这可以通过关注重要变量和交互来更快地进行属性预测。我们用它来研究elpasolite宇宙，对低地层能量结构进行集中搜索。

虽然对非线性解使用事后可解释性方法有助于分析，但能够使用线性模型的系数要简单得多，并且不需要进一步计算，还说明了函数形式。可视化数百个变量与预测结果之间的关系比用定义明确的公式描述关系更复杂。交互检测可以使用事后可解释性方法进行，但可能需要昂贵或复杂的技术。使用符号回归或SISSO的方法也具有列出的特征。然而，当有大量特征时，自动搜索分析公式可能会变得非常昂贵。此外，分析包含数百个具有多种不同转换的基函数的模型变得极具挑战性。因此，这些技术尚未用于本研究中研究的应用。相反，我们使用了数量少得多的可能运算符，这些运算符由物理洞察力指导。我们还关注具有大量特征的数据集，在这些数据集中，尚未意识到非线性基函数的简单线性组合会产生准确的预测模型。

本研究有助于建立复杂的非线性机器学习方法在预测化学和材料特性方面的能力。通过为这些具有挑战性的任务生成专门的线性解决方案，我们提供了有关这些预测模型如何工作的新见解，并证明更改所使用的回归模型类型可能是实现可解释性的可行途径。广义非线性解将为各种问题提供准确的模型，但使用更专业的回归模型可以提供比准确性更多的好处。这已经从线性原子间势的发展以及相关的速度和外推的改进中看出。在这里，我们展示了预测线性解的可解释性的好处。

图文速览

关于可解释性的探讨自然引出了对其潜在价值的分析。我们可以列举诸多优点，比如深化科学认知、增强可信度、揭示新的化学与物理规律以及扩充知识储备。不过，我们并未停留在抽象概念的讨论上，而是具体归纳了以下关键特征及其关联优势：

1） 通过解析线性模型的系数，能够验证模型是否符合已知物理定律。后续案例将展示，这实际上构成了一种物理行为的检验方法。以elpasolite晶体为例，其形成能在元素周期表中的变化趋势就能通过线性模型系数直观呈现。

2） 明确的函数表达式可以揭示模型隐含的基本假设。这为新模型与传统预测方法的对比提供了可能，有助于识别其中的物理假设，进而判断模型的适用边界。当把TCO的求解过程转化为特定线性模型时，既能发现与材料建模中经典团簇展开法的共通点，也能预测模型适用的材料体系。

3） 模型系数蕴含的规律能为后续预测提供指导。聚焦关键变量及其相互作用可加速性能预测。我们已将此方法应用于elpasolite体系，实现了对低形成能结构的定向筛选。

研究团队首先分析了NOMAD Kaggle竞赛优胜模型对TCO形成能的预测案例，该模型采用n-grams作为特征表达方法。

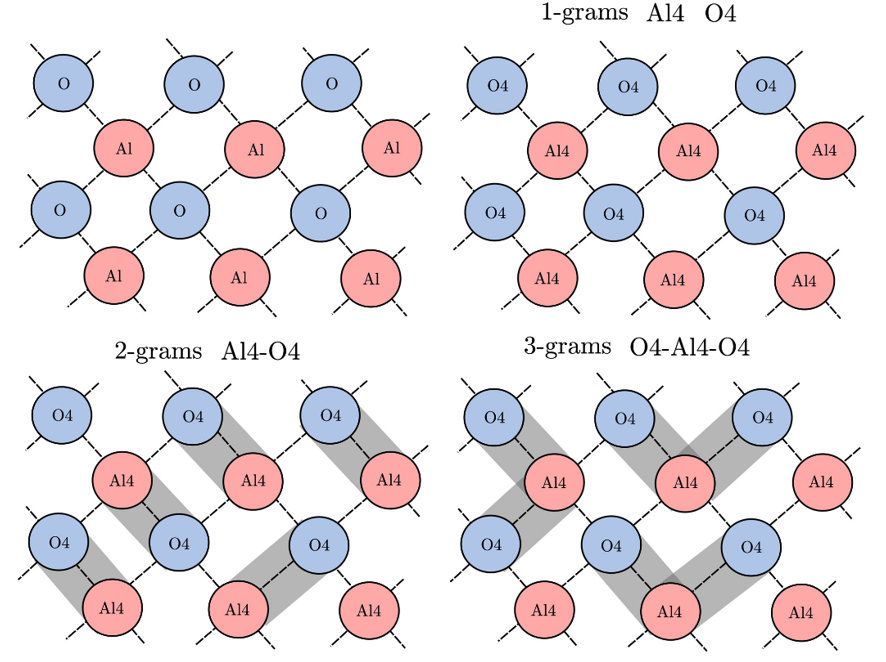
图 1.n-gram表示法的图解

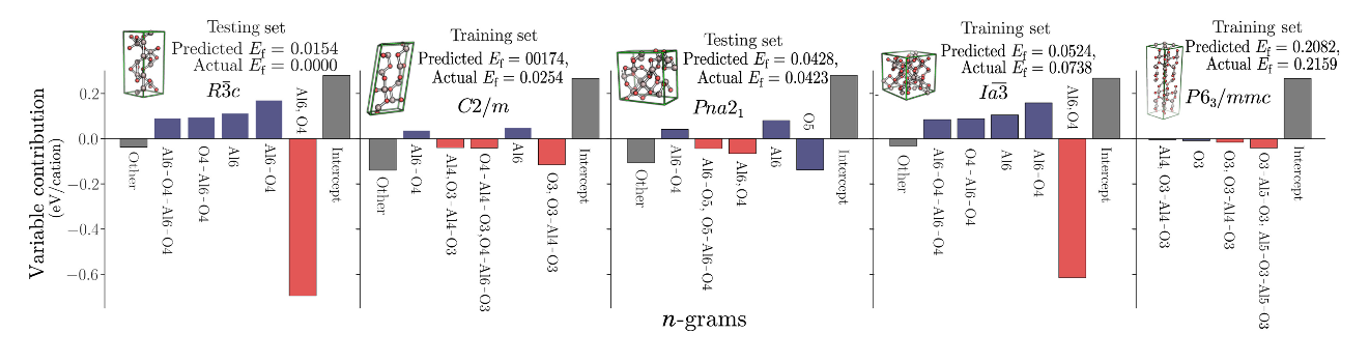
图 2.氧化铝多晶型物的可变贡献

对于五个Al₂O₃多晶型物在透明导电氧化物数据集中，显示了前五个变量对预测形成能的贡献，还给出了其余的贡献和截距。这些可以由a_ix_i或β_ijx_ix_j从双线性模型中直接计算出来，而预测的能量只是所有变量贡献的总和。交互作用项以红色显示，主效应以蓝色显示。

为验证核方法求解结果是否与n-gram线性模型具有相似性，研究者采用事后可解释技术对形成能的核解进行了可视化。通过绘制部分依赖（PD）图表征变量与机器学习结果的平均关联，基于一组KRR模型的分析揭示了解的多样性。为确保趋势的稳健性，需要评估解对微小扰动的敏感性。图3展示了三个变量的核模型PD图。

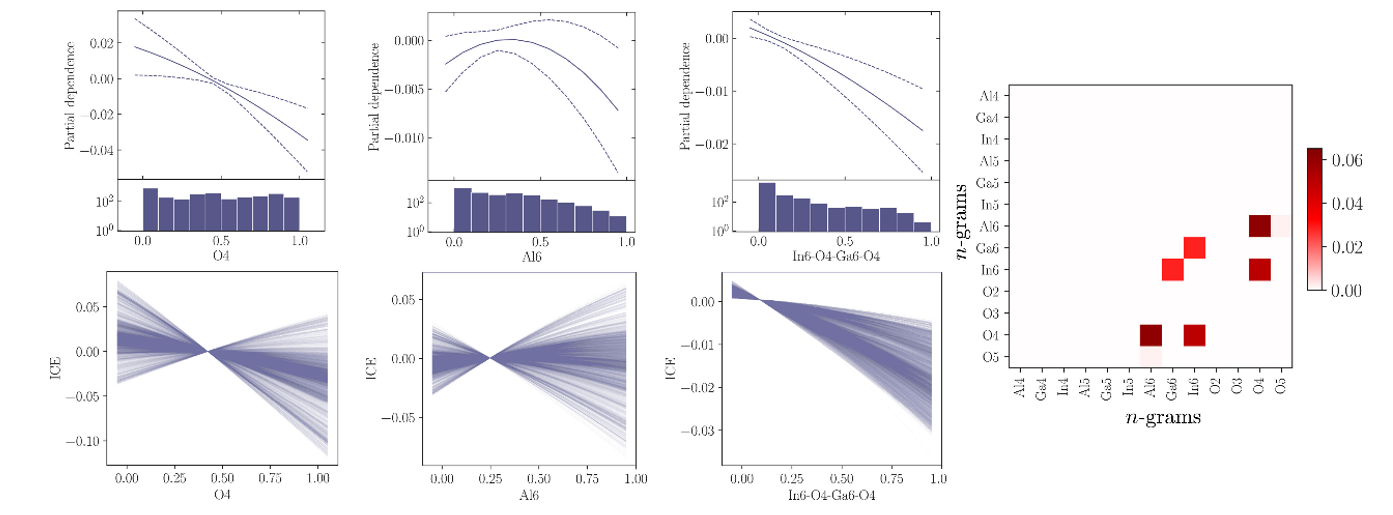
图 3.KRR TCO 模型的 PD、ICE 和交互作用

使用线性模型的系数，可以分离每种元素对形成能的贡献，根据图4可以看出，位点D的碳对形成能的贡献最大，而位点D的氟贡献最小。这种趋势反映了氟更喜欢形成异核键而不是同核键，而碳更喜欢形成同核键。此外，还可以计算各个系数的贡献。

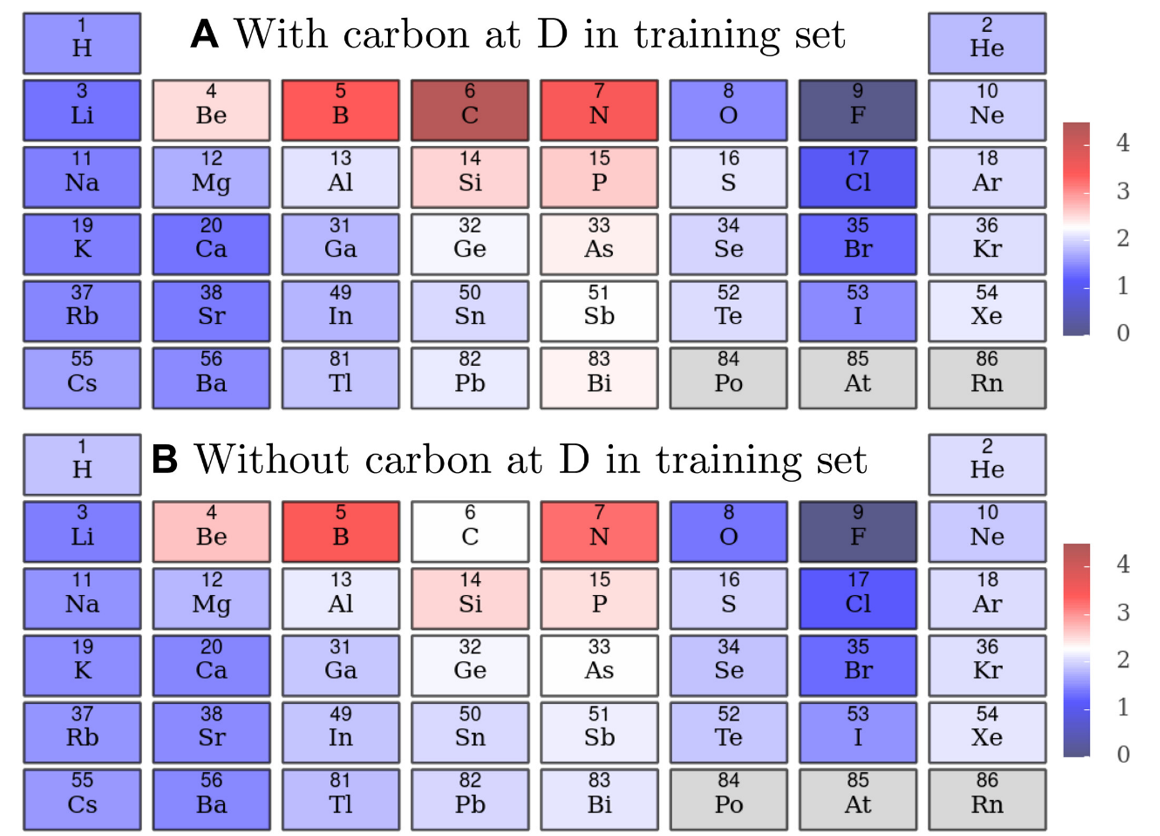
图 4.位点D对元素周期表中形成能量的贡献

位点D每个原子的形成能量（以电子伏特/原子为单位），用于（A）训练集中包含碳的模型和（B）位置D处训练集中不包含碳的模型。这是直接从模型的系数计算的，零点设置为氟的最低值。

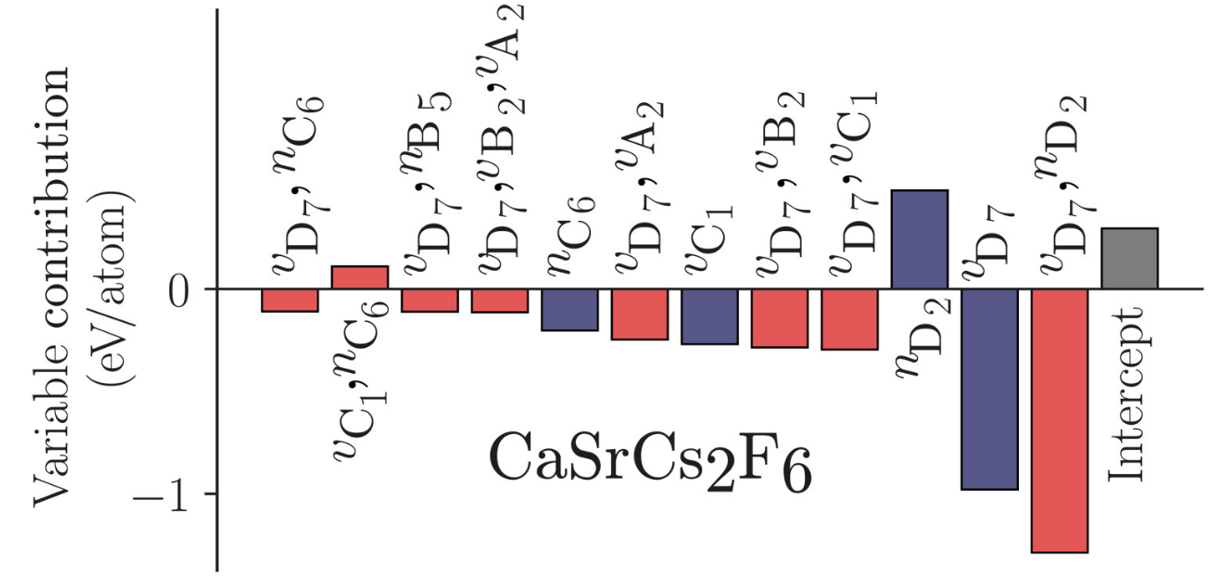
图 5. CaSrCs₂F₆晶体形成能的变量贡献分解

可解释机器学习的重要价值在于指导材料预测。例如，elpasolite线性模型的系数能高效定位值得深入研究的结构区域。以低形成能elpasolite筛选为例，初级策略可能仅关注含氟的D位点。但若仅考虑单一位点信息，模型会推荐FFBa₂F₆结构——这并非低能构型，因其忽略了位点间的键合作用。因此必须引入交互项，而这在非线性模型中难以直观实现。三变量线性模型则能通过系数呈现丰富的结构信息。

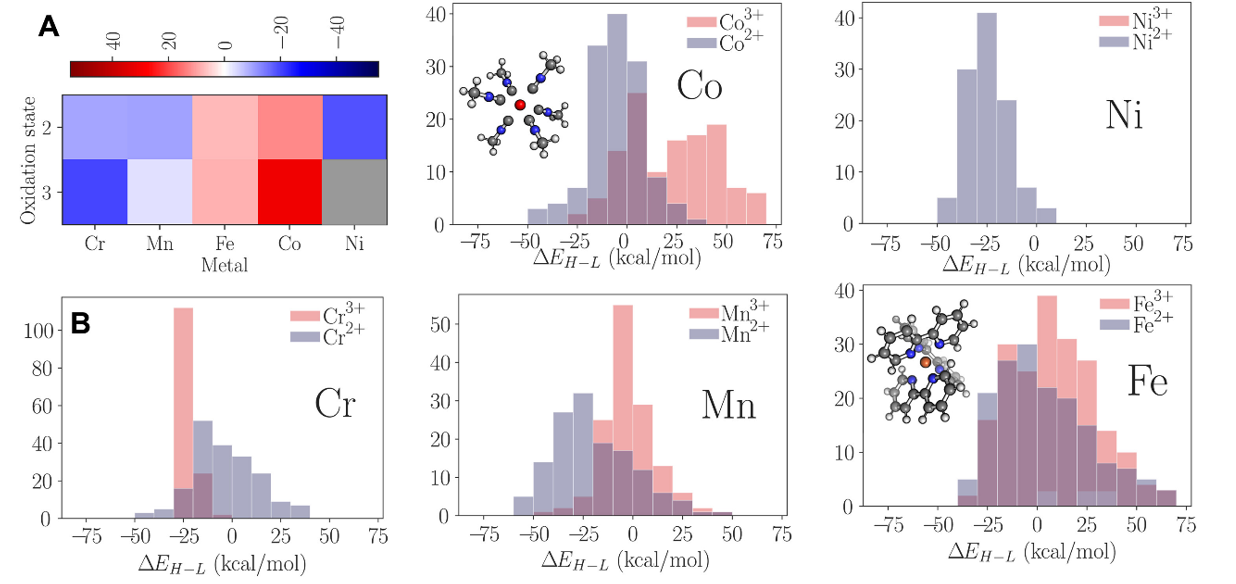
图 6.过渡金属配合物的模型系数和数据集分布

（A）金属和氧化态对预测自旋分裂的贡献。灰色表示 Ni³⁺在数据集中不存在。（B）分布在ΔE_{H − L}数据集中的不同金属离子。如果差值为正，则自旋配置较低，如果差值为负，则自旋配置较高。

线性与非线性模型的关联可通过多种解析方法建立。例如，多项式核与线性模型存在精确等价关系，其他核类型也可构造线性近似。可视化非线性解为比较两类模型提供了新思路，PD和ICE方法都能刻画变量与预测值的关联。当非线性解呈现明确规律时，可据此构建对应的线性模型。图7的模拟数据PD与ICE图便展示了这一过程。

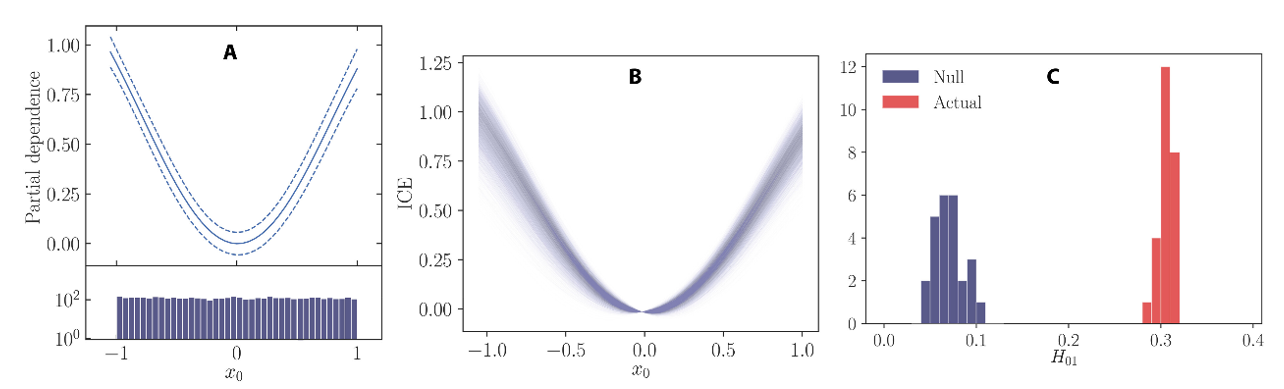
图 7.模拟数据的 PD、ICE 和交互检测示例

x₀的（A） PD和（B）ICE图。模拟数据的形式为，其中，x₀是从−1和1之间的均匀概率分布中得出的，ε∼N（0,0.25）。虚线显示 95%置信区间，实线是五个模型拟合的平均值。使用NN模型。PD将其居中绘制，以便PD（0）= 0作为集成的平均值。ICE 图居中，以便。（C）实系综模型的H统计量分布和拟合的NN系综模型的空分布。

当然，并非所有问题都适用这种简化。比如原子间势或仅凭化学计量预测形成能等问题，难以在保证精度的前提下建立可解释模型。虽然原子间势的线性模型形式更为复杂，其线性特性仍能提供部分洞见，但解析难度远高于本书所述的简单线性模型。因此，区分需要复杂非线性解与适合简单线性解的应用场景至关重要——后者往往能构建本质可解释模型，而回归模型的复杂度决定了实现可解释性的最佳途径。

本研究选取的案例展示了机器学习助力材料与分子性质预测的典型范例，但实践证明，简单回归模型同样能胜任这些任务。无论是探索elpasolite体系、预测过渡金属配合物自旋态，还是在NOMAD Kaggle竞赛中获胜，黑箱模型并非唯一选择。当明确变量特性并理解基础物理原理时，简单线性方案往往能实现相当的预测性能。专用回归模型具有多重优势：线性原子间势在运算效率和外推性上表现更优，而简单线性模型则充分发挥了可解释性优势。

研究价值

该研究通过开发可解释的多线性模型，在材料机器学习领域实现了预测性能与物理透明度的双重突破。与传统“黑箱”模型相比，该方法通过线性组合非线性基函数，在保持预测精度的同时，赋予模型系数明确的物理意义，可直接关联材料成分、结构与性能的定量关系。研究验证了“简单模型优先”的可行性，证明在离散变量主导或数据集有限时，线性模型可替代复杂非线性方法，显著降低计算成本。研究进一步提出跨领域方法迁移框架，为融合数据驱动与机理模型指明方向。未来，该方法可拓展至能源材料、生物材料等领域，推动材料发现从“试错式实验”向“可解释AI驱动”的范式转型。

文章小结

本文通过构建可解释的线性组合模型，在材料科学领域实现了预测精度与物理解释的协同优化。以Elpasolite晶体为例，模型通过变量贡献分解定量揭示了材料性质与结构特征间的关联规律，预测误差降至0.11 eV/atom，同时提供明确的物理洞察。研究还验证了数据驱动与物理先验的融合价值：在过渡金属配合物自旋态预测中，模型系数直接反映配体场理论（如Cr³⁺的高自旋倾向），误差较神经网络降低30%（2.2 kcal/mol）。通过多保真数据融合（如DFT计算与实验数据），该方法显著降低了高精度模拟成本，为电催化剂活性位点设计、磁性材料筛选等提供了高效工具。

原文链接：https://www.science.org/doi/10.1126/sciadv.abm7185